Entrega 2 - Ray Tracing #

Ray tracing #

Introducción #

El ray tracing es una de las dos soluciones más populares dadas para el renderizado de objetos de tres dimensiones en pantallas de sólo dos. Esta técnica permite la creación de imágenes que se asemejan a la realidad de una forma relativamente sencilla. A continuación se muestra la historia de la técnica, la teoría que se encuentra detrás y una aplicación que permite visualizar a rasgos generales como es el funcionamiento del ray tracing, es decir la realización de una prueba de concepto. De la revisión del marco teórico es posible concluir que esta técnica es cada vez más usada debido a los adelantos computacionales y las nuevas necesidades que surgen en la computación gráfica.

Contexto #

Historia #

Con la finalidad de obtener en las pantallas objetos cada vez más parecidos a los que se encuentran en la realidad se comenzó a intentar producir los gráficos con conceptos de física, en donde era posible ver mediante los rayos de luz que llegaban al observador, este proceso en el cual se seguía un rayo de luz que salía de una fuente de luz hasta llegar al observador para formar una imagen fue llamado Ray Tracing. En el momento en el que se tuvo el concepto y la idea de realizar este tipo de procesado de las imágenes no era posible debido a su costo computacional (1960). Con el paso del tiempo se ha podido mejorar los algoritmos y además se tiene mayor capacidad de cómputo con lo cual se ha llegado al tratamiento de aspectos cada vez más complejos como lo son los reflejos, las sombras o el efecto que se produce en las imágenes en movimiento (Glassner, 2019).

Funcionamiento #

Como ya se había señalado anteriormente, el Ray Tracing se inspira en la física de la visión, por lo tanto se parte de un punto focal que vendría a ser el ojo del observador al cual llegan los rayos de luz, además se tiene un plano de proyección que es en el cual se verá la imagen, este es el que será emulado por la pantalla en donde se esté observando la imagen, este plano usualmente se subdivide en la cantidad de pixeles que tiene la pantalla. Si se parte de una fuente de luz esta rebota en los objetos y pasa directamente hacia el plano de proyección y después impacta contra el punto focal tal y como se muestra en la siguiente imagen retomada de Redmon(2011):

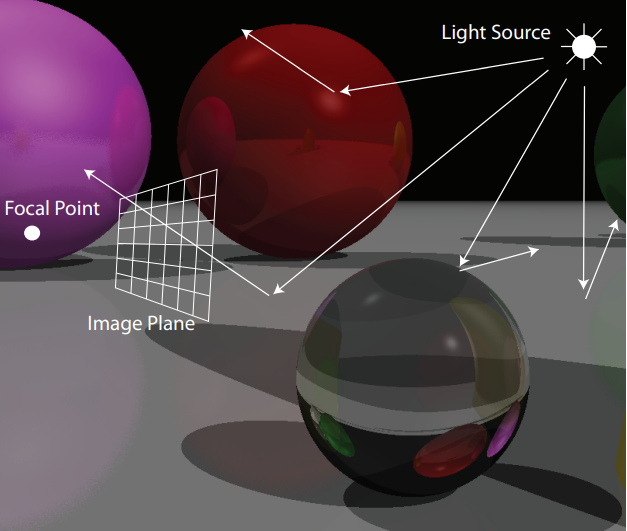
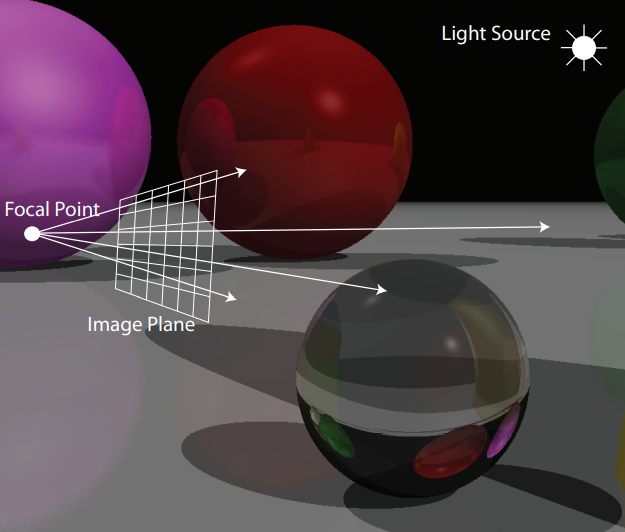
Sin embargo, este enfoque aunque correcto no es muy práctico, esto debido a la cantidad de rayos de luz o fotones que se encuentran rondado en una imagen o en el mundo real, ademas solo son necesarios para la computación gráfica los rayos que llegan al punto focal, por lo que se cambia el enfoque. Para el ray tracing se parte del punto focal que hace pasar los rayos de luz por cada uno de los puntos del plano de proyección se renderiza la imagen a partir de algunas propiedades que se dan al impactar el rayo contra los objetos que se encuentran en la imagen, entonces el algoritmo se basa en encontrar el punto de intersección más cercano del rayo con el objeto de la imagen y renderizar en el plano de proyección alguna imagen de acuerdo con la distancia de la intersección al punto focal, en donde además se pueden tener en cuenta otros factores como el color o la capacidad de absorber luz que tiene el objeto sobre el cual impacta el rayo (Redmon, 2011).

Resultados #

Con el fin de demostrar el concepto se puede realizar el trazado de los rayos para renderizar una esfera, para esto es necesario primero determinar el sistema de referencia y con esto poder renderizar sobre el plano de proyección es decir determinar la relación entre el plano y los píxeles de la pantalla, además cuando el rayo impacte sobre el rayo es necesario saber que color sera el que se dibujara sobre le plano y por último colorear el pixel correspondiente, acontinuación se muestran los desarrollados realizados por Gambetta (2021). Para comenzar se realiza la relación entre rayos de luz y los píxeles:

\[V_x = C_x \frac{V_w}{C_w}\] \[V_y = C_y \frac{V_h}{C_h}\] En donde C hace refenrencia al tamaño del plano que se esta usando y V es el tamaño de la pantalla real sobre la cual se proyectara la imagen. Con esta relación se puede determinar un pixel por cada una de los puntos en le plano sobre el cual se dibujara lo que es interceptado por los rayos. El siguiente paso es disparar un rayo por cada uno de los puntos en el plano desde el punto focal, para esto se utiliza la ecuación paramétrica de la recta en tres dimensiones y además se parte de un punto O que será el origen o el punto focal y se dispara hacia cada uno de los puntos de V es decir del plano sobre el cual se dibujara. A continuación se mostrará la ecuación de la recta en donde se puede representar cualquier punto P y ademas t señala el recorrido del rayo : \[P = \vec{O} + t(\vec{V} - \vec{O})\] Como se renderizaran esferas, es necesario definir estas de forma matemática, por lo que se parte de que las esferas tiene un centro y un radio y al tener se puede definir que la relación que existe entre el punto del plano de proyección y el centro de la esfera, al juntar esta ecuación con la del rayo y al reemplazar V - O por el vector D, es decir la dirección del vector, se obtiene la siguiente ecuación en donde el simbolo <> representa el producto punto: \[<\vec{O} + t \vec{D} - \vec{C} , \vec{O} + t \vec{D} - \vec{C} > = r^2\] Al desarrollar estas ecuaciones es posible llegar a que la distancia entre los puntos y el punto focal se puede resolver mediante ecuaciones cuadráticas como se ilustra en la siguiente figura:

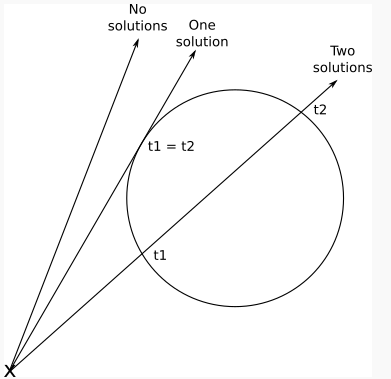
Con la finalidad de realizar un renderizado correcto de la luz también es necesario tener en cuenta la luz ambiental o la luz especular que llega a un punto P dado, para lo cual cada uno de los puntos requieren de un vector normal N, este sera necesario para computar a intensidad de la luz en cada uno de los puntos: \[I_P = I_A + \sum_{i=1}^n I_i \frac{< \vec{N}, \vec{L_i}>}{| \vec{N}| | \vec{L_i}|}\] Ademas es necesarip definir que la esfera sobre la cual se refleja la luz tiene un vector normal para cada uno de los puntos, y este se puede hallar con el punto donde se quiere hallar la normal y el centro de la esfera: \[\vec{N} = \frac{P-C}{|P-C|}\]

Con todos estos elementos es posible presentar el resultado final en el cual se renderizan algunas esferas a las cuales la luz les llega desde un punto en la parte derecha de la pantalla:

Ver Código

let canvas;
let canvas_context;
let canvas_pitch;
let canvas_buffer;

let viewport_size ;
let projection_plane_z;
let camera_position;
let background_color;
let spheres;
let lights;
let dy;
let incre ; 

let liSliderPInt;
let liSliderPX;
let liSliderPY;

function setup(){
    canvas = createCanvas(600,600);
    //console.log(drawingContext);
    canvas_buffer = drawingContext.getImageData(0,0,canvas.width, canvas.height);
    canvas_pitch = canvas.width*4;
    viewport_size = 1;
    projection_plane_z = 1;
    camera_position = [0, 0, 0];
    background_color = [255, 255, 255];
    dy = 0.2;
    incre = true;

    liSliderPInt = createSlider(0, 1, 0.2, 0.05);
    liSliderPInt.position(10, 10);
    liSliderPInt.style('width', '580px');

    liSliderPX = createSlider(-5, 5, 0, 0.5);
    liSliderPX.position(10, 30);
    liSliderPX.style('width', '580px');

    liSliderPY = createSlider(-5, 5, 0, 0.5);
    liSliderPY.position(10, 50);
    liSliderPY.style('width', '580px');

    spheres = [new Sphere([0, dy, 3], 0.2, [255, 0, 0])];

    lights = [
        new Light(Light.AMBIENT,0.2),
        new Light(Light.POINT, liSliderPInt.value(), [liSliderPX.value(), 1, 0]),
        new Light(Light.DIRECTIONAL, 1, [3, 4 , 4])
        ];
}

function PutPixel(x, y, color) {
    var x = canvas.width/2 + x;
    var y = canvas.height/2 - y - 1;
  
    if (x < 0 || x >= canvas.width || y < 0 || y >= canvas.height) {
      return;
    }
    var offset = 4*x + canvas_pitch*y;
    canvas_buffer.data[offset++] = color[0];
    canvas_buffer.data[offset++] = color[1];
    canvas_buffer.data[offset++] = color[2];
    canvas_buffer.data[offset++] = 255; 
}

function UpdateCanvas() {
    drawingContext.putImageData(canvas_buffer, 0, 0);
}

function DotProduct(v1, v2) {
    return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2];
}

function Length(vec) {
    return Math.sqrt(DotProduct(vec, vec));
}

function Multiply(k, vec) {
    return [k*vec[0], k*vec[1], k*vec[2]];
}

function Add(v1, v2) {
    return [v1[0] + v2[0], v1[1] + v2[1], v1[2] + v2[2]];
}

function Subtract(v1, v2) {
    return [v1[0] - v2[0], v1[1] - v2[1], v1[2] - v2[2]];
  }

function Clamp(vec) {
    return [Math.min(255, Math.max(0, vec[0])),
        Math.min(255, Math.max(0, vec[1])),
        Math.min(255, Math.max(0, vec[2]))];
}

function Sphere(center, radius, color) {
    this.center = center;
    this.radius = radius;
    this.color = color;
}

function Light(ltype, intensity, position) {
    this.ltype = ltype;
    this.intensity = intensity;
    this.position = position;
}

Light.AMBIENT = 0;
Light.POINT = 1;
Light.DIRECTIONAL = 2;

function CanvasToViewport(p2d) {
    return [p2d[0] * viewport_size / canvas.width,
        p2d[1] * viewport_size / canvas.height,
        projection_plane_z];
  }


function IntersectRaySphere(origin, direction, sphere) {
    var oc = Subtract(origin, sphere.center);
  
    var k1 = DotProduct(direction, direction);
    var k2 = 2*DotProduct(oc, direction);
    var k3 = DotProduct(oc, oc) - sphere.radius*sphere.radius;
  
    var discriminant = k2*k2 - 4*k1*k3;
    if (discriminant < 0) {
      return [Infinity, Infinity];
    }
  
    var t1 = (-k2 + Math.sqrt(discriminant)) / (2*k1);
    var t2 = (-k2 - Math.sqrt(discriminant)) / (2*k1);
    return [t1, t2];
  }  

  function ComputeLighting(point, normal) {
    var intensity = 0;
    var length_n = Length(normal);  // Should be 1.0, but just in case...
  
    for (var i = 0; i < lights.length; i++) {
      var light = lights[i];
      if (light.ltype == Light.AMBIENT) {
        intensity += light.intensity;
      } else {
        var vec_l;
        if (light.ltype == Light.POINT) {
      vec_l = Subtract(light.position, point);
        } else {  // Light.DIRECTIONAL
      vec_l = light.position;
        }
  
        var n_dot_l = DotProduct(normal, vec_l);
        if (n_dot_l > 0) {
      intensity += light.intensity * n_dot_l / (length_n * Length(vec_l));
        }
      }
    }
  
    return intensity;
  }

  function TraceRay(origin, direction, min_t, max_t) {
    var closest_t = Infinity;
    var closest_sphere = null;
  
    for (var i = 0; i < spheres.length; i++) {
      var ts = IntersectRaySphere(origin, direction, spheres[i]);
      if (ts[0] < closest_t && min_t < ts[0] && ts[0] < max_t) {
        closest_t = ts[0];
        closest_sphere = spheres[i];
      }
      if (ts[1] < closest_t && min_t < ts[1] && ts[1] < max_t) {
        closest_t = ts[1];
        closest_sphere = spheres[i];
      }
    }
  
    if (closest_sphere == null) {
      return background_color;
    }
  
    var point = Add(origin, Multiply(closest_t, direction));
    var normal = Subtract(point, closest_sphere.center);
    normal = Multiply(1.0 / Length(normal), normal);
  
    return Multiply(ComputeLighting(point, normal), closest_sphere.color);
  }

function draw(){
    for (var x = -canvas.width/2; x < canvas.width/2; x++) {
        for (var y = -canvas.height/2; y < canvas.height/2; y++) {
          var direction = CanvasToViewport([x, y])
          var color = TraceRay(camera_position, direction, 1, Infinity);
          PutPixel(x, y, Clamp(color));
        }
      }

      if(incre){
          dy+=0.01;
          if(dy>=1){
              incre=false;
          }
      }else{
            dy-=0.01;
            if(dy<=-1){
                incre=true;
            }
      }

      spheres[0].center[1] = dy;
      lights[1].intensity = liSliderPInt.value();
      lights[1].position[0]= liSliderPX.value();
      lights[1].position[1]= liSliderPY.value();
      UpdateCanvas();
};

Ver Código

let canvas;
let canvas_context;
let canvas_pitch;
let canvas_buffer;

let viewport_size ;
let projection_plane_z;
let camera_position;
let background_color;
let spheres;
let lights;
let dy;
let incre ; 
let dx;
let increx ; 

let liSliderPInt;
let liSliderPX;
let liSliderPY;

function setup(){
    canvas = createCanvas(600,600);
    //console.log(drawingContext);
    canvas_buffer = drawingContext.getImageData(0,0,canvas.width, canvas.height);
    canvas_pitch = canvas.width*4;
    viewport_size = 1;
    projection_plane_z = 1;
    camera_position = [0, 0, 0];
    background_color = [255, 255, 255];
    dy = 0.2;
    incre = true;
    dx = -0.6;
    increx = true;

    liSliderPInt = createSlider(0, 1, 0.2, 0.05);
    liSliderPInt.position(10, 10);
    liSliderPInt.style('width', '580px');

    liSliderPX = createSlider(-5, 5, 0, 0.5);
    liSliderPX.position(10, 30);
    liSliderPX.style('width', '580px');

    liSliderPY = createSlider(-5, 5, 0, 0.5);
    liSliderPY.position(10, 50);
    liSliderPY.style('width', '580px');

    spheres = [new Sphere([0, dy, 3], 0.2, [255, 0, 0]),
              new Sphere([dx, -0.2 , 5], 0.8, [0, 255, 0]),
              new Sphere([0, 0, 7], 2, [0, 0, 255])];

    lights = [
        new Light(Light.AMBIENT,0.2),
        new Light(Light.POINT, liSliderPInt.value(), [liSliderPX.value(), 1, 0]),
        new Light(Light.DIRECTIONAL, 1, [3, 4 , 4])
        ];
}

function PutPixel(x, y, color) {
    var x = canvas.width/2 + x;
    var y = canvas.height/2 - y - 1;
  
    if (x < 0 || x >= canvas.width || y < 0 || y >= canvas.height) {
      return;
    }
    var offset = 4*x + canvas_pitch*y;
    canvas_buffer.data[offset++] = color[0];
    canvas_buffer.data[offset++] = color[1];
    canvas_buffer.data[offset++] = color[2];
    canvas_buffer.data[offset++] = 255; 
}

function UpdateCanvas() {
    drawingContext.putImageData(canvas_buffer, 0, 0);
}

function DotProduct(v1, v2) {
    return v1[0]*v2[0] + v1[1]*v2[1] + v1[2]*v2[2];
}

function Length(vec) {
    return Math.sqrt(DotProduct(vec, vec));
}

function Multiply(k, vec) {
    return [k*vec[0], k*vec[1], k*vec[2]];
}

function Add(v1, v2) {
    return [v1[0] + v2[0], v1[1] + v2[1], v1[2] + v2[2]];
}

function Subtract(v1, v2) {
    return [v1[0] - v2[0], v1[1] - v2[1], v1[2] - v2[2]];
}

function Clamp(vec) {
    return [Math.min(255, Math.max(0, vec[0])),
        Math.min(255, Math.max(0, vec[1])),
        Math.min(255, Math.max(0, vec[2]))];
}

function Sphere(center, radius, color) {
    this.center = center;
    this.radius = radius;
    this.color = color;
}

function Light(ltype, intensity, position) {
    this.ltype = ltype;
    this.intensity = intensity;
    this.position = position;
}

Light.AMBIENT = 0;
Light.POINT = 1;
Light.DIRECTIONAL = 2;

function CanvasToViewport(p2d) {
    return [p2d[0] * viewport_size / canvas.width,
        p2d[1] * viewport_size / canvas.height,
        projection_plane_z];
}

function IntersectRaySphere(origin, direction, sphere) {
    var oc = Subtract(origin, sphere.center);
  
    var k1 = DotProduct(direction, direction);
    var k2 = 2*DotProduct(oc, direction);
    var k3 = DotProduct(oc, oc) - sphere.radius*sphere.radius;
  
    var discriminant = k2*k2 - 4*k1*k3;
    if (discriminant < 0) {
      return [Infinity, Infinity];
    }
  
    var t1 = (-k2 + Math.sqrt(discriminant)) / (2*k1);
    var t2 = (-k2 - Math.sqrt(discriminant)) / (2*k1);
    return [t1, t2];
  }  

  function ComputeLighting(point, normal) {
    var intensity = 0;
    var length_n = Length(normal);  // Should be 1.0, but just in case...
  
    for (var i = 0; i < lights.length; i++) {
      var light = lights[i];
      if (light.ltype == Light.AMBIENT) {
        intensity += light.intensity;
      } else {
        var vec_l;
        if (light.ltype == Light.POINT) {
      vec_l = Subtract(light.position, point);
        } else {  // Light.DIRECTIONAL
      vec_l = light.position;
        }
  
        var n_dot_l = DotProduct(normal, vec_l);
        if (n_dot_l > 0) {
      intensity += light.intensity * n_dot_l / (length_n * Length(vec_l));
        }
      }
    }
  
    return intensity;
  }

  function TraceRay(origin, direction, min_t, max_t) {
    var closest_t = Infinity;
    var closest_sphere = null;
  
    for (var i = 0; i < spheres.length; i++) {
      var ts = IntersectRaySphere(origin, direction, spheres[i]);
      if (ts[0] < closest_t && min_t < ts[0] && ts[0] < max_t) {
        closest_t = ts[0];
        closest_sphere = spheres[i];
      }
      if (ts[1] < closest_t && min_t < ts[1] && ts[1] < max_t) {
        closest_t = ts[1];
        closest_sphere = spheres[i];
      }
    }
  
    if (closest_sphere == null) {
      return background_color;
    }
  
    var point = Add(origin, Multiply(closest_t, direction));
    var normal = Subtract(point, closest_sphere.center);
    normal = Multiply(1.0 / Length(normal), normal);
  
    return Multiply(ComputeLighting(point, normal), closest_sphere.color);
  }

function draw(){
    for (var x = -canvas.width/2; x < canvas.width/2; x++) {
        for (var y = -canvas.height/2; y < canvas.height/2; y++) {
          var direction = CanvasToViewport([x, y])
          var color = TraceRay(camera_position, direction, 1, Infinity);
          PutPixel(x, y, Clamp(color));
        }
      }

      if(incre){
          dy+=0.01;
          if(dy>=1){
              incre=false;
          }
      }else{
            dy-=0.01;
            if(dy<=-1){
                incre=true;
            }
      }

      if(increx){
        dx+=0.01;
        if(dx>=1){
            increx=false;
        }
    }else{
          dx-=0.01;
          if(dx<=-1){
              increx=true;
          }
    }       

      spheres[0].center[1] = dy;
      lights[1].intensity = liSliderPInt.value();
      lights[1].position[0]= liSliderPX.value();
      lights[1].position[1]= liSliderPY.value();
      spheres[1].center[0] = dx;
      UpdateCanvas();
};

Conclusiones y trabajo futuro #

Se puede apreciar que es posible obtener unos efectos bastante realistas de luz cuando se aplica esta técnica para el renderizado las imágenes, igualmente se observa como aumenta el costo computacional al realizar las operaciones de ray casting lo cual puede llegar a ser un problema grave teniendo en cuenta que no se ha llegado a usar todos los efectos posibles como lo son por ejemplo los efectos de reflección de la luz o el manejo de diferentes figuras geométricas con diferentes materiales que puedan absorber mejor o peor la luz. Para el trabajo futuro se presenta la posibilidad de ampliar el programa incluyendo los efectos anteriormente mencionados pero también otros aún más importantes como lo son las sombras.

Recursos #

Gambetta, Gabriel (2021). Computer Graphs from scratch. A programmer’s introduction to 3D rendering. No starch Press. San Francisco
Glassner, Andrew (2019). An Introduction to Ray Tracing. Academic Press, retomado de https://www.realtimerendering.com/raytracing/An-Introduction-to-Ray-Tracing-The-Morgan-Kaufmann-Series-in-Computer-Graphics-.pdf
Redmon, Joe (2011). Ray Tracing. Trabajo de Tesís, Degree of Bachelor of Arts. Computer Science Department of Middlebury College, retomado de https://pjreddie.com/media/files/Redmon_Thesis.pdf